3 min to read
Everything is matter
Reflections on the blog "Attention and Linear Regression"
In the blog post “Attention and Linear Regression”, a fascinating claim is made: attention and linear regression share similar mathematical structures—most notably matrix operations involving dot products and normalization—yet behave very differently in practice. This insight led me to a deeper realization:
Everything is matter. Not just the mathematical forms, but the underlying context, mechanisms, and behavior.
Introduction
Motivated by this observation, I re-implemented and significantly extended the idea using PyTorch, creating a full pipeline that compares attention mechanisms to linear regression, both mathematically and empirically. The goal was not only reproduction, but also exploration—of different data types, model configurations, and operational nuances.
This experiment investigates how changes in architecture (e.g., whitening, shared weights) and loss behavior affect the alignment between attention and regression, especially under different data regimes.
Experimental Design
Data Modes
- Synthetic Linear Data: Controlled environment with known ground-truth weights and structured feature correlation.
- Real Data: Diabetes dataset from scikit-learn, scaled and split.
- Simple Data: A toy example using sine activation to inject nonlinearity.
Attention Variants
- Vanilla Attention: Softmax over scaled dot products.
- Regression-like Attention: Removes softmax, approximating linear projection behavior.
- Whitened Attention: Applies data whitening to decorrelate inputs, simulating assumptions in linear regression.
Architectural Choices
- With / Without Whitening: Use of whitening matrix derived from eigendecomposition of covariance.
- Shared vs. Separate Weight Matrices: Determines whether $Wq$ and $Wk$ are tied.
Comparison Baseline
Ridge Regression: With a small L2 regularization ($λ = 1 \times 10^{-3}$) to ensure numerical stability. Serves as the ground truth in both synthetic and real settings.
Core Analyses
1. Prediction Accuracy
For each configuration, I computed MSE (mean squared error) on both training and test sets. Attention models were compared to ridge regression not just by raw accuracy, but also by cosine similarity of outputs.
2. Projection Matrix Comparison
The projection behavior was analyzed by comparing:
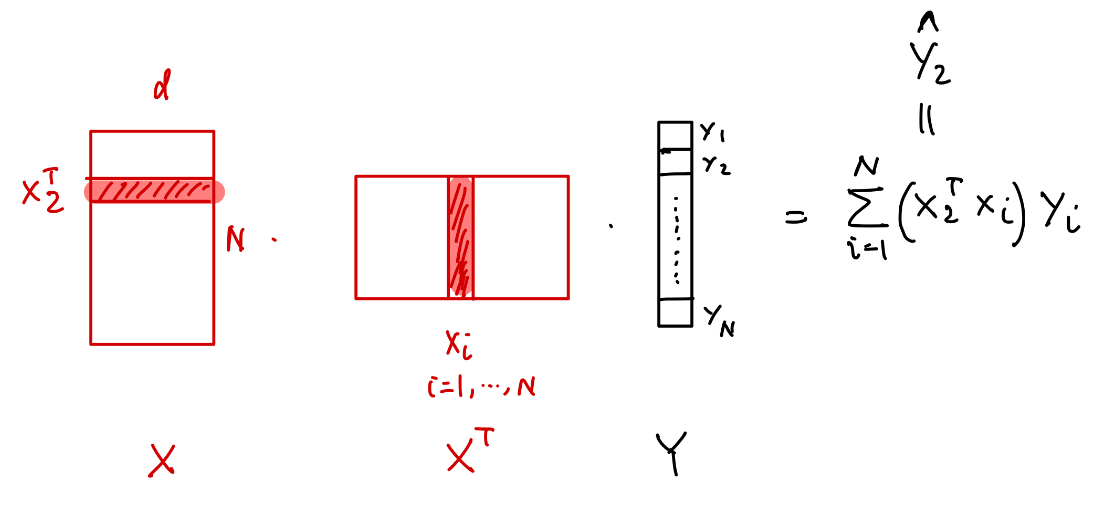
- Hat Matrix ($H$) from ridge regression: $X(X^TX + λI)^{-1}X^T$
- Attention Weight Matrix (A): learned during training
- Raw Scores ($QK^T$)
- Weight Composition ($W_qW_k^T$)
These matrices were visualized side-by-side to inspect similarities and divergences in projection behavior.
3. Effective Weights
In synthetic settings, where true weights are known, I compared:
- True Weights
- Estimated Weights from Ridge Regression
- Effective Weights from Attention: calculated via $W_{combined} X^T Y / d_{features}$
This gives insight into what the attention model “learns” implicitly.
Highlights & Observations
Even when attention and regression achieve similar output quality, their mechanisms differ starkly:
- Regression uses a global, closed-form mapping.
- Attention operates locally, relying on similarity or context via softmax or whitening.
Closing Thoughts
This exploration confirms the original blog’s thesis, but in a more empirical and systematic way. The core operations may look similar (dot products, projections), but their semantics and emergent behaviors differ.
- Attention isn’t just a “fancy matrix multiplication”, it adapts to local or learned similarity, which can align—but does not have to.
- Linear regression isn’t “just another dot product model”, it makes assumptions about global structure.
They reflect different philosophies: one built on analytic closure, the other on contextual flexibility.
Same math ≠ same meaning, structure matters—but behavior matters more.